In 1622, Frans van Schooten sr. wrote on f113^r of his lecture notes:

During the preceding years, professor Van Schooten had handwritten his carefully constructed and elaborately illustrated lecture notes on mathematics and surveying in the same book, which is present as BPL 1013 in the University Library. In November 1622 he started writing and illustrating the second part of his teaching task, on fortification. From 1611-1645 Van Schooten taught an engineering course in the Dutch language; both the contents and teaching language were very unusual for a respectable university at the time.

Mathematics formed part of the undergraduate programme, the Liberal Arts, at most universities. Mathematics courses consisted of lectures, in Latin, on pure mathematics (number theory and Euclidean geometry) and mixed mathematics, subjects such as astronomy, mechanics, and cosmography. These lectures were based on classical texts by Greek and Arabic authors, translators, and commentators. The mathematics taught was primarily theoretical, without attention to possible practical use.

Separate from this learned world a practical form of mathematics was used by common people who did not know Latin: practitioners such as surveyors, bookkeepers, building masters, military architects, traders, and navigators. The mathematics taught to these people, was primarily practical, without much attention to theoretical background, tending to the learning of tricks that seemed to work in practice.

There were, however, a few exceptions with regards to knowledge of mathematical theory. Some mathematical practitioners, such as the military engineers Adriaan Antonisz. and Samuel Crop and the mathematics teacher Ludolf van Ceulen, based their practices on sound theoretical mathematical knowledge, without knowledge of Latin.

Just after its founding, Leiden University needed to attract a good number of students as fast as possible, so the curators did their utmost to find professors with a good reputation. It is rather fascinating that only 25 years after the university’s founding, the curators were willing to take a risk concerning the academic reputation of the university, by offering a new course in practical mathematics (surveying and fortification), taught in Dutch instead of the academic Latin. Consequently, this course, commonly named the Duytsche Mathematique, could not lead to a university degree.

What were the reasons for this unusual academic enterprise and how did this course relate to the academic mathematics programme?

During the first years after the founding, there was no professor for the undergraduate mathematics courses, mathematics had a lower priority than subjects such as theology, logic, dialectics, and in Leiden especially, the classical and eastern languages. In 1581 Rudolph Snellius was appointed; he had a degree in liberal arts from the Calvinist University at Marburg. Snellius taught a broad range of mathematical subjects, based on works by Petrus Ramus (an educational innovator who proposed a shorter, more condensed, and well-structured curriculum) and the works of the classical authors. Around 1605, Rudolph Snellius gave lectures on geometry, geography, and optics, while his son Willebrord assisted him with lectures on arithmetic and astronomy. Willebrord Snellius was a respected and productive mathematician, who succeeded his father as professor in 1613. He taught the theory through the classical authors but also used mathematics to solve practical problems, such as the development of an improved technique of triangulation in surveying, using his own big quadrant to measure distances. In 1629 Jacob Golius, an expert in Arabic languages and literature, who purchased many Arabic manuscripts for the university, became his successor.

Towards the end of the sixteenth century Maurits and Willem Lodewijk van Nassau, commanders of the Dutch army, realized they would need many more mathematically trained engineers and surveyors to maintain their military advantage over the Spanish army. At Leiden University, Maurits, together with his tutor and engineer Simon Stevin, convinced the curators to establish a separate course, taught in Dutch, for surveyors and military engineers. The course officially started in January 1600, with a curriculum formulated by Stevin in the Instruction. Maurits and Stevin were enrolled as students at Leiden during the early 1580s when Rudolph Snellius was still primarily teaching Petrus Ramus’ works. The Instruction prescribes an efficient curriculum, with a combination of theory and practice; a method of study much favoured by Stevin.

The first professors teaching Duytsche Mathematique were Ludolf van Ceulen and Simon Fransz. van Merwen. Ludolf van Ceulen was a respected mathematical practitioner, who taught mathematics and fencing and served on some committees advising the government. He didn’t know any Latin but was very accomplished in geometry. He is best known for his calculation of the first 35 decimals of π.

In December 1610 Van Ceulen passed away, whereupon his former student, assistant, surveyor and military engineer, Frans van Schooten, continued the lectures and the practice sessions in the field, as a temporary lecturer. In 1615 Frans van Schooten was appointed professor Duytsche Mathematique.

Thanks to his lecture notes, BPL 1013, we have an idea of the contents and excellent structure of the course. First, the students were taught arithmetic and geometry. Calculating square and cubic roots, how to perform all calculations using only decimal numbers and calculations in geometrical forms. Geometry consisted of a rather limited selection from the books of Euclid, constructions, and transformations. This was followed by the practice of surveying, including the use of trigonometric tables.

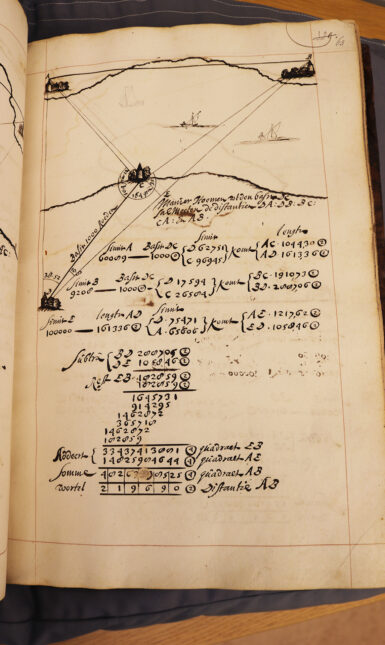
Van Schooten continued with advanced surveying techniques and advanced geometry, in which various geometric techniques to calculate heights and distances were practised.

The surveyor’s part of the course ended with calculations of volumes and wine gauging. Students who had come this far could take an exam to become admitted surveyors. The second part of BPL 1013 deals with Fortification, defined by Van Schooten as the art of building and defending fortifications as well as the art of attacking and conquering fortified places.

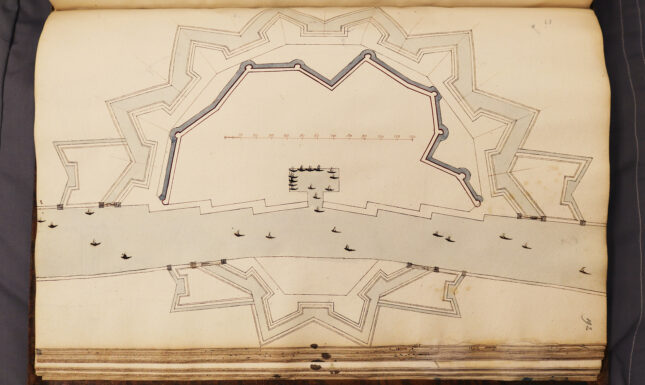
In 1646 Frans van Schooten sr. was succeeded by his eldest son, Frans van Schooten jr., a very talented mathematician, who translated Descartes’ Geometry into Latin.

Both the regular undergraduate course and the engineering course were taught by excellent teachers, who were in their time considered to be good to excellent mathematicians. The contents of the courses, however, were quite different. One could say that the Latin courses taught the theory of mathematics as developed by Greek authors, whereas the Dutch engineering course taught how to use mathematics in a responsible way, based on reliable theory. Both seem to have attracted a good number of students and contributed to the good reputation of the university.

____

Dr Jenneke Krüger is an independent researcher, connected to the Utrecht University Freudenthal Institute. In 2014 she wrote her PhD thesis on the history of mathematics education in the Netherlands.